3ND

夏が終わった

首页 归档 标签 关于

RSA Crypto System Study Note

2019-12-17 13 min read # Crypto # Course

0x01 前言

RSA 加密算法是一种非对称加密演算法，在公开密钥加密和电子商业中被广泛使用。RSA 是 1977 年由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)一起提出的。当时他们三人都在麻省理工学院工作。RSA 就是他们三人姓氏开头字母拼在一起组成的。

RSA 应用广泛，但在实际中却常用于：数据小片段的加密，尤其用于密钥传输和数字签名。RSA 加密的本意并不是为了取代对称密码，而且它比诸如 AES 的密码要慢很多，这主要是因为 RSA (或其他公钥算法)执行中涉及很多计算。其加密特征的主要用途就是安全地交换对称密码的密钥，通常与类似 AES 的对称密码一起使用，其中真正用于加密大量数据的是对称密码。

RSA 底层的单向函数是整数因式分解问题：两个大素数相乘在计算上是非常简单的，但是对其乘积进行因式分解确是十分困难的。欧拉定理和欧拉函数在 RSA 中发挥着至关重要的作用。

0x02 加密解密

RSA 加密和解密都是在整数环 Zn\mathbb{Z}_{n} 内完成的，模运算在其中发挥了核心作用。

RSA 加密 给定公钥 (n,e)=kpub(n, e)=k_{pub} 和明文 xx，则加密函数为:

y = e_{k_{pub\}\}(x) \equiv x^{e} \ mod \ n

其中 x,y∈Znx, y ∈ \mathbb{Z}_{n}.

RSA 解密 给定私钥 d=kprd = k_{pr} 及密文 yy，则解密函数为：

x = d_{k_{pr\}\}(y) \equiv y^{d} \ mod \ n

其中 x,y∈Znx, y ∈ \mathbb{Z}_{n}.

RSA 密码体制的一些需求：

  1. 由于攻击者可以得到公钥，所以，对于给定的公钥值 ee 和 nn，确定私钥 dd 在计算上必须是不可行的；

  2. 由于 xx 知识唯一取决于模数 nn 的大小，所以一次 RSA 加密的位数不能超过 ll，其中 ll 指 nn 的位长度。

  3. 计算 $ x^{e} \ mod \ n $ 和 $ y^{d} \ mod \ n$ 应该相对简单，这意味着我们需要一种能够快速计算长整数的指数的方法。

  4. 给定一个 nn 应该能对应很多公钥/秘钥对，否则，攻击者就可以发起蛮力攻击（事实上这个需求很容易被满足）。

0x03 密钥生成

生成步骤

输出： 公钥：kpub=(n,e)k_{pub} = (n, e) 和私钥：kpr=(d)k_{pr} = (d).

  1. 选择两个大素数 pp 和 qq ；

  2. 计算 n=p⋅qn = p · q ；

  3. 计算 φ(n)=(p−1)(q−1)\varphi(n)=(p-1)(q-1) ；

  4. 选择满足以下条件的公开指数 e∈1,2,...,ϕ(n)−1e\in \\{ 1,2,...,\phi(n)-1 \\}

gcd(e,ϕ(n))=1gcd(e,\phi(n)) = 1

保证 ee 模 ϕ(n)\phi(n) 存在逆元，即私钥 dd 始终存在。

  1. 计算满足以下条件的私钥 dd

d⋅e≡1 mod ϕ(n)d · e \equiv 1 \ mod \ \phi(n)

大素数生成

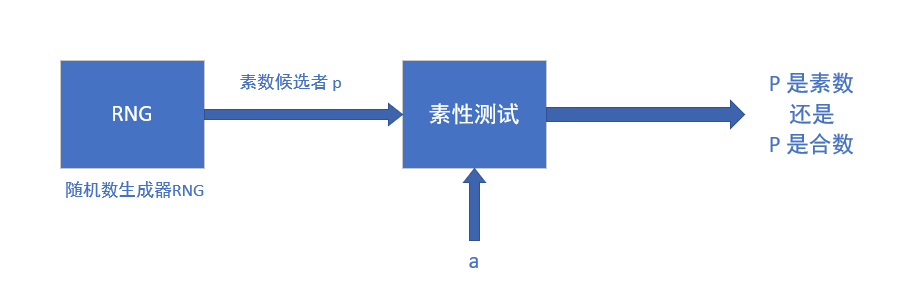
密钥生成的步骤 1 中生成了素数 pp 和素数 qq ， 这两个素数的乘积就是 RSA 模数 n=p⋅qn=p·q，并且它们的长度应该是 nn 的位长度的一半。例如，如果我们想建立一个模长度为 ⌈log⁡2n⌉=1024\lceil \log_{2}n\rceil=1024 的 RSA，pp 、qq 对应的位长度为 512。最通用的方法就是随机生成整数，然后进行素性检验。其中随机数生成器 RNG 必须是不可预测的，否则攻击者计算或猜测出其中一个素数就可以轻而易举地破解 RSA 。

素数的普遍性 随机选择的奇数 pp 为素数的概率为：

P(p为素数)≈2ln(p)P\left( p 为素数\right) \approx \dfrac {2}{ln\left( p\right) }

选择某个整数为素数的概率与整数的位长度成正比，因而下降缓慢，这意味着即使对非常长的 RSA 参数，比如 4096 位，素数的密度依然足够高。

素性测试

费马素性测试

根据费马小定理：如果 p 是素数，1≤a≤p−11\leq a\leq p-1，那么

{\displaystyle a^{p-1}\equiv 1{\pmod {p\}\}}

如果我们想知道 nn 是否是素数，我们在中间选取 a，看看上面等式是否成立。如果对于数值 a 等式不成立，那么 n 是合数。如果有很多的 a 能够使等式成立，那么我们可以说 n 可能是素数，或者伪素数。

在我们检验过程中，有可能我们选取的 a 都能让等式成立，然而 n 却是合数。这时等式

{\displaystyle a^{n-1}\equiv 1{\pmod {n\}\}}

被称为 Fermat liar，n 为卡迈尔克数。如果我们选取满足下面等式的 a

{\displaystyle a^{n-1}\not \equiv 1{\pmod {n\}\}}

那么 a 也就是对于 n 的合数判定的 Fermat witness。

如果一个卡迈尔克数的质因子都非常大，费马测试能检测出该值真的是合数的基数 aa 非常少，因此，实际中常采用功能更加强大的 Miller-Rabin 测试来生成 RSA 素数。

Miller-Rabin 素性测试

Miller-Rabin 质数判定法是一种质数判定法则，利用随机化算法判断一个数是合数还是可能是素数。

定理 给定一个奇素数候选者 pp 的分解：

p−1=2urp-1=2^{u}r

其中 rr 是奇数。如果可以找到一个整数 aa，使得

a^{r} \not \equiv 1 \ mod \ p \ 且 \ a^{r2^{j\}\} \not \equiv p-1 \ mod \ p

对所有的 j=0,1,...,u−1j=\\{0,1,...,u-1\\} 都成立，则 pp 为一个合数，否则，它可能是一个素数。

from random import randrange, randint

# Miller-Rabin Primality Test
def Miller_Rabin(n, s=77):
    if n % 2 == 0:
        return False
    if n == 2 or n == 3:
        return True
    u, r = 0, n - 1
    while r % 2 == 0:
        u += 1
        r //= 2
    for _ in range(s):
        a = randrange(2, n - 2)
        z = pow(a, r, n)
        if z != 1 and z != n - 1: # j = 0
            for j in range(1, u - 1):
                z = pow(z, 2, n)
                if z == 1:
                    return False
            if z != n - 1:
                return False
    return True

# Generate l-bit Prime Number
def genPrime(l=1024):
    while True:
        # MSB(1) -> n-bit; LSB(1) Tail Odd Number 
        randm = int("1".join([str(randint(0, 1)) for _ in range(l - 2)]) + "1", 2)
        if Miller_Rabin(randm):
            return randm

EEA - 拓展欧几里得

拓展欧几里得算法(EEA, Extended Euclidean Algorithm) 到目前为止，我们发现两个整数 r0r_{0} 和 r1r_{1} 的 gcd 最大公因数的计算可以通过不断迭代地减小操作数来实现。欧几里得算法的主要应用并不是计算 gcd ，拓展欧几里得算法可以用来计算模逆元。

gcd(r0,r1)=s⋅r0+t⋅r1gcd(r_{0}, r_{1}) = s·r_{0} + t · r_{1}

其中 s 和 t 均为整型系数，该方程通常称为丢番图方程(Diophantine equation)。如何获取系数 s 和 t ？此算法的思路为执行标准欧几里得算法，但将每轮迭代中的余数 rir_{i} 表示为如下形式的线性组合：

ri=sir0+tir1r_{i} = s_{i}r_{0} + t_{i}r_{1}

则最后一轮迭代对应的等式为：

rl=gdc(r0,r1)=slr0+tlr1=sr0+tr1r_{l}=gdc(r_{0},r_{1})=s_{l}r_{0}+t_{l}r_{1}=sr_{0}+tr_{1}

这也意味着最后一个系数 sls_{l} 也就是上述等式所寻找的系数 ss，同时 tl=tt_{l}=t。

# Extended Euclidean Algorithm
def Exgcd(r0, r1):
    # r0*si + r1*ti = ri
    if r1 == 0:
        return (1, 0, r0)
    # r0*s1 + r1*t1 = r0
    s1, t1 = 1, 0
    # r0*s2 + r1*t2 = r1
    s2, t2 = 0, 1
    while r1 != 0:
        q = r0 / r1
        # ri = r(i-2) % r(i-1)
        r = r0 % r1
        r0, r1 = r1, r
        # si = s(i-2) - q*s(i-1)
        s = s1 - q*s2
        s1, s2 = s2, s
        # ti = t(i-2) - q*t(i-1)
        t = t1 - q*t2
        t1, t2 = t2, t
    return(s1, t1, r0)

- 完整代码 -:

# -*- coding: utf-8 -*-

from random import randrange, randint

# Miller-Rabin Primality Test
def Miller_Rabin(n, s=77):
    if n % 2 == 0:
        return False
    if n == 2 or n == 3:
        return True
    u, r = 0, n - 1
    while r % 2 == 0:
        u += 1
        r //= 2
    for _ in range(s):
        a = randrange(2, n - 2)
        z = pow(a, r, n)
        if z != 1 and z != n - 1: # j = 0
            for j in range(1, u - 1):
                z = pow(z, 2, n)
                if z == 1:
                    return False
            if z != n - 1:
                return False
    return True

# Generate l-bit Prime Number
def genPrime(l=1024):
    while True:
        # MSB(1) -> n-bit; LSB(1) Tail Odd Number 
        randm = int("1".join([str(randint(0, 1)) for _ in range(l - 2)]) + "1", 2)
        if Miller_Rabin(randm):
            return randm

# String to Hex
def str2hex(m):
    return "".join("{:02x}".format(ord(x)) for x in m)

# Extended Euclidean Algorithm
def Exgcd(r0, r1):
    # r0*si + r1*ti = ri
    if r1 == 0:
        return (1, 0, r0)
    # r0*s1 + r1*t1 = r0
    s1, t1 = 1, 0
    # r0*s2 + r1*t2 = r1
    s2, t2 = 0, 1
    while r1 != 0:
        q = r0 / r1
        # ri = r(i-2) % r(i-1)
        r = r0 % r1
        r0, r1 = r1, r
        # si = s(i-2) - q*s(i-1)
        s = s1 - q*s2
        s1, s2 = s2, s
        # ti = t(i-2) - q*t(i-1)
        t = t1 - q*t2
        t1, t2 = t2, t
    return(s1, t1, r0)

# computeD: Known phi(n) and e, calculate d
# d ≡ e'(mod phi(n))
# e: the public (or encryption) exponent
# phi_n:  Euler totient function phi(n) = (p-1)*(q-1)
def computeD(e, phi_n):
    (s, t, r) = Exgcd(phi_n, e)
    # t maybe < 0, so convert it
    return t if t > 0 else phi_n + t

# Generate the encryption index: e
# 通常来说，e 不需要太大，这样可以大幅提高加密效率。
# 我们可以生成一个素数，若它不是 φ(n) 的因数，则(e, φ(n))=1
def genE(phi_n):
    while True:
        e = genPrime(l=randint(3,13))
        if e == 3 or e == 5:
            continue
        if phi_n % e != 0:
            return e

# RSA Encryption
# Public key: (n,e)
# c ≡ m^e (mod n)
def RSAEncrypt(message, e, n):
    message = int(str2hex(message), 16)
    print "message = " + str(message)
    cipher = pow(message, e, n)
    return cipher

# RSA Decryption
# Private published: true
hideInList: false
feature: 
isTop: false
# m ≡ c^d (mod n)
def RSADecrypt(cipher, d, n):
    message = pow(cipher, d, n)
    message = '{:x}'.format(message).decode('hex')
    return message

def main():
    # 生成两个大素数 p 和 q
    print "[+] Generate p and q:"
    p = genPrime(512)
    q = genPrime(512)
    print "> p = " + str(p)
    print "> q = " + str(q)
    # 计算 n = p * q
    n = p * q
    print "> n = " + str(n)
    # 计算 φ(n) = (p - 1) * (q - 1)
    phi_n = (p - 1) * (q - 1)
    print "[+] Generate e Now ..."
    # 生成一个和φ(n)互素的数e
    e = genE(phi_n)
    print "> e = " + str(e)
    message = raw_input("Please Input Message >> ")
    # 加密算法
    print "[+] Encrypt Message Now ..."
    Ciphertext = RSAEncrypt(message, e, n)
    print "> Ciphertext is: " + str(Ciphertext)
    # 解密算法
    print "[+] Decrypt CipherText Now ..."
    # 使用私钥 d，d 是 e 模 φ(n) 的逆
    d = computeD(e, phi_n)
    print "> d = " + str(d)
    Plaintext = RSADecrypt(Ciphertext, d, n)
    print "> Plaintext is:" + str(Plaintext)

if __name__ == "__main__":
    main()

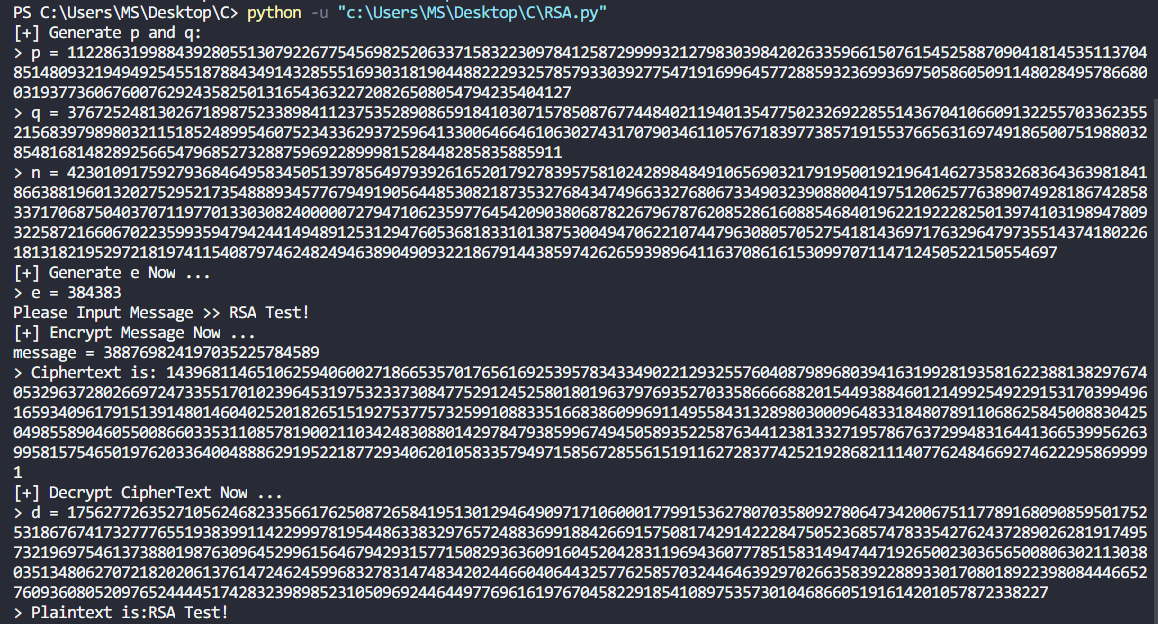
运行测试：

RSS