3ND

夏が終わった

首页 归档 标签 关于

Message-Digest Algorithm 5 - MD5

2019-12-24 17 min read # Crypto # Course

0x01 MD5 概述

Hash 函数是一个非常重要的密码学组件，在协议中广泛使用。哈希函数计算了一个消息的摘要，而这个摘要是一个非常短的、固定长度的位字符串。对某个特定的消息而言，哈希摘要（或哈希值）可以看做是该消息的指纹，即消息的唯一表示。Hash 函数时数字签名方案和消息验证码的核心部分，在其他密码学应用中也得到广泛使用，比如存储密码的哈希或密钥衍生。

MD5 消息摘要算法（MD5 Message-Digest Algorithm），一种被广泛使用的密码散列函数，可以产生出一个 128-bit（16-byte，1-byte = 8-bit，1个16进制位-> 4-bit，通常使用 32 位的十六进制位表示，方便查看。）的散列值（hash value），用于确保信息传输完整一致。MD5 由美国密码学家罗纳德·李维斯特（Ronald Linn Rivest）设计，于 1992 年公开，用以取代 MD4 算法。这套算法的程序在 RFC 1321 中被加以规范。

0x02 算法流程

MD5 是输入不定长度信息，输出固定长度 128-bits 的算法。经过程序流程，生成四个 32 位数据，最后联合起来成为一个 128-bits 散列。基本方式为，求余、取余、调整长度、与链接变量进行循环运算，得出结果。

class MD5(object):
    _string = None
    _buffers = {
        MD5Buffer.A: None,
        MD5Buffer.B: None,
        MD5Buffer.C: None,
        MD5Buffer.D: None,
    }

附加填充位

首先填充 1 个 1 和 若干个 0 使得消息长度（包括原始消息的长度和本次填充的长度）模 512 与 448 同余。
* 需要特别注意的是，若原始消息长度刚好满足模 512 与 448 同余，则还需要填充 1 个 1 和 511 个 0 。

@classmethod
def _step_1(cls):
    # Convert the string to a bit array.
    # 将字符串转化为二进制数组(Big-endian)
    bit_array = bitarray(endian="big")
    bit_array.frombytes(cls._string.encode("utf-8"))
    # Pad the string with a 1 bit and as many 0 bits required such that
    # the length of the bit array becomes congruent to 448 modulo 512.
    # Note that padding is always performed, even if the string's bit
    # length is already conguent to 448 modulo 512, which leads to a
    # new 512-bit message block.
    bit_array.append(1)
    while bit_array.length() % 512 != 448:
        bit_array.append(0)
    # For the remainder of the MD5 algorithm, all values are in
    # little endian, so transform the bit array to little endian.
    return bitarray(bit_array, endian="little")

再将原始长度以 64-bit（小端序）表示附加在填充结果的后面，从而使得最终的长度（包括原始消息的长度、本次填充的长度和 64-bit 的消息长度）是 512-bit 的倍数。

@classmethod
def _step_2(cls, step_1_result):
    # Extend the result from step 1 with a 64-bit little endian
    # representation of the original message length (modulo 2^64).
    length = (len(cls._string) * 8) % pow(2, 64)
    length_bit_array = bitarray(endian="little")
    # format:"<Q"; <:Little-endian; Q: unsigned long long;
    length_bit_array.frombytes(struct.pack("<Q", length))
    result = step_1_result.copy()
    result.extend(length_bit_array)
    return result

初始化链接变量

class MD5Buffer(Enum):
    A = 0x67452301
    B = 0xEFCDAB89
    C = 0x98BADCFE
    D = 0x10325476
# Class MD5(Object)
@classmethod
def _step_3(cls):
    # Initialize the buffers to their default values.
    for buffer_type in cls._buffers.keys():
        cls._buffers[buffer_type] = buffer_type.value

分组处理

MD5 以 512-bit 为分组长度进行分组。每个分组又被分成 16 * 32-bit 的子分组，分别参与每轮的 16 个步骤。

# Process chunks of 512 bits.
for chunk_index in range(N // 16):
    # Break the chunk into 16 words of 32 bits in list X.
    start = chunk_index * 512
    X = [step_2_result[start + (x * 32) : start + (x * 32) + 32] for x in range(16)]
    # Convert the `bitarray` objects to integers.
    X = [int.from_bytes(word.tobytes(), byteorder="little") for word in X]

歩函数

该算法包括 4 轮，每轮 16 步：

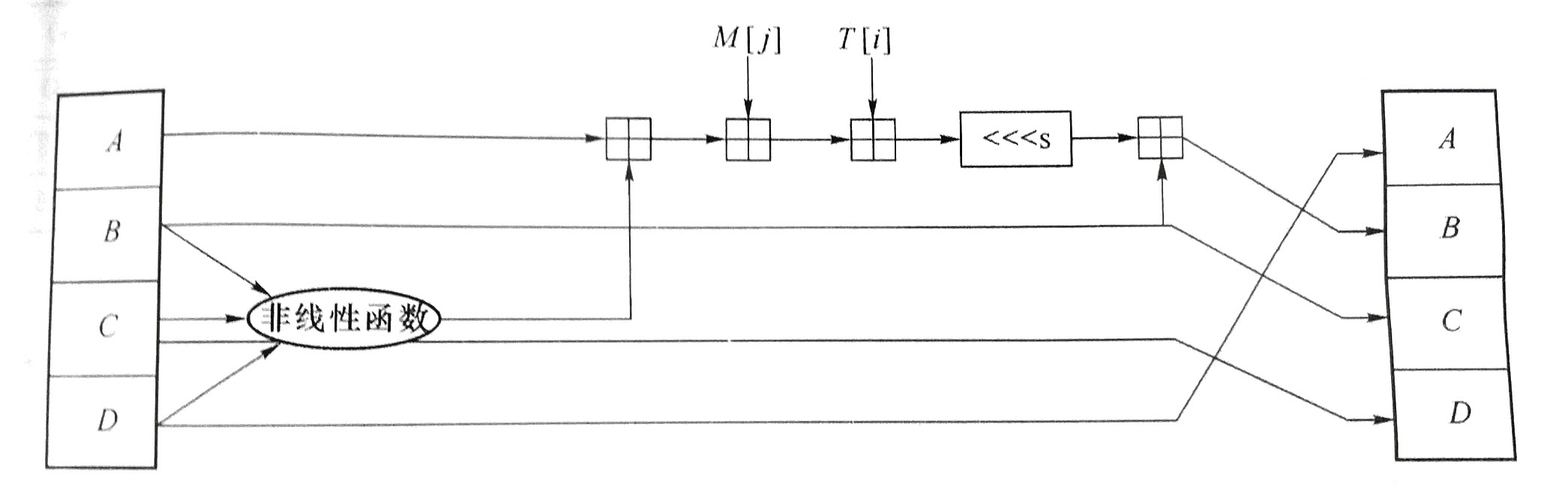
  1. 上一步的链接变量 D, B, C 直接赋值给下一步的链接变量 A, C, D。即 D -> A、B -> C、C -> D。

  2. A 先和非线性函数的结果相加，结果再和 M[j] 相加，结果再和 T[i]相加，结果再循环左移 s 次，得到的结果再和原来的 B 相加，最后的得到新 B。

A + func_output + M[j] + T[i] -> <<< s -> + B -> B

非线性函数

  • F(X,Y,Z)=(X∧Y)∨(¬X∧Z)F(X,Y,Z)=(X\wedge {Y})\vee (\neg {X}\wedge {Z})
  • G(X,Y,Z)=(X∧Z)∨(Y∧¬Z)G(X,Y,Z) = (X\wedge{Z}) \vee (Y \wedge \neg{Z})
  • H(X,Y,Z)=X⊕Y⊕ZH(X,Y,Z) = X \oplus Y \oplus Z
  • I(X,Y,Z)=Y⊕(X∨¬Z)I(X,Y,Z) = Y \oplus (X \vee \neg{Z})

其中 ⊕、∧、∨、¬\oplus、 \wedge、 \vee、 \neg 分别是 XOR、 AND、 OR、 NOT 的符号。

# Define the four auxiliary functions that produce one 32-bit word.
F = lambda x, y, z: (x & y) | (~x & z)
G = lambda x, y, z: (x & z) | (y & ~z)
H = lambda x, y, z: x ^ y ^ z
I = lambda x, y, z: y ^ (x | ~z)

M[j]、T[i]

M[j] 即前面说的消息分组的 32 bit 子分组。第一轮中就是简单的 0, 1, …, 15，后面 3 轮的次序由以下置换确定：

  • $P_{2}(i) = (1 + 5i) \ mod \ 16 $
  • $P_{3}(i) = (5 + 3i) \ mod \ 16 $
  • $P_{4}(i) = 7i \ mod \ 16 $

T[i] 为常数:

T[i]=[232×abs(sin(i))]=[4294967296×abs(sin(i))]T[i]=[2^{32}×abs(sin(i))]=[4294967296×abs(sin(i))]

其中 i 为弧度，方框代表取整。

# Compute the T table from the sine function. Note that the
# RFC starts at index 1, but we start at index 0.
T = [floor(pow(2, 32) * abs(sin(i + 1))) for i in range(64)]

循环左移

4 轮次 16 步中循环左移的位数是根据规定计算的，计算并移位即可，循环移位函数如下：

# Define the left rotation function, which rotates `x` left `n` bits.
rotate_left = lambda x, n: (x << n) | (x >> (32 - n))

歩函数 Python 代码实现：

@classmethod
def _step_4(cls, step_2_result):
    # Define the four auxiliary functions that produce one 32-bit word.
    F = lambda x, y, z: (x & y) | (~x & z)
    G = lambda x, y, z: (x & z) | (y & ~z)
    H = lambda x, y, z: x ^ y ^ z
    I = lambda x, y, z: y ^ (x | ~z)
    # Define the left rotation function, which rotates `x` left `n` bits.
    rotate_left = lambda x, n: (x << n) | (x >> (32 - n))
    # Define a function for modular addition.
    modular_add = lambda a, b: (a + b) % pow(2, 32)
    # Compute the T table from the sine function. Note that the
    # RFC starts at index 1, but we start at index 0.
    T = [floor(pow(2, 32) * abs(sin(i + 1))) for i in range(64)]
    # The total number of 32-bit words to process, N, is always a
    # multiple of 16.
    N = len(step_2_result) // 32
    # Process chunks of 512 bits.
    for chunk_index in range(N // 16):
        # Break the chunk into 16 words of 32 bits in list X.
        start = chunk_index * 512
        X = [step_2_result[start + (x * 32) : start + (x * 32) + 32] for x in range(16)]
        # Convert the `bitarray` objects to integers.
        X = [int.from_bytes(word.tobytes(), byteorder="little") for word in X]
        # Make shorthands for the buffers A, B, C and D.
        A = cls._buffers[MD5Buffer.A]
        B = cls._buffers[MD5Buffer.B]
        C = cls._buffers[MD5Buffer.C]
        D = cls._buffers[MD5Buffer.D]
        # Execute the four rounds with 16 operations each.
        for i in range(4 * 16):
            if 0 <= i <= 15:
                k = i
                s = [7, 12, 17, 22]
                temp = F(B, C, D)
            elif 16 <= i <= 31:
                k = ((5 * i) + 1) % 16
                s = [5, 9, 14, 20]
                temp = G(B, C, D)
            elif 32 <= i <= 47:
                k = ((3 * i) + 5) % 16
                s = [4, 11, 16, 23]
                temp = H(B, C, D)
            elif 48 <= i <= 63:
                k = (7 * i) % 16
                s = [6, 10, 15, 21]
                temp = I(B, C, D)
            # The MD5 algorithm uses modular addition. Note that we need a
            # temporary variable here. If we would put the result in `A`, then
            # the expression `A = D` below would overwrite it. We also cannot
            # move `A = D` lower because the original `D` would already have
            # been overwritten by the `D = C` expression.
            temp = modular_add(temp, X[k])
            temp = modular_add(temp, T[i])
            temp = modular_add(temp, A)
            temp = rotate_left(temp, s[i % 4])
            temp = modular_add(temp, B)
            # Swap the registers for the next operation.
            A = D
            D = C
            C = B
            B = temp
        # Update the buffers with the results from this chunk.
        cls._buffers[MD5Buffer.A] = modular_add(cls._buffers[MD5Buffer.A], A)
        cls._buffers[MD5Buffer.B] = modular_add(cls._buffers[MD5Buffer.B], B)
        cls._buffers[MD5Buffer.C] = modular_add(cls._buffers[MD5Buffer.C], C)
        cls._buffers[MD5Buffer.D] = modular_add(cls._buffers[MD5Buffer.D], D)

经过 4×16 次迭代后，我们可以得到最后的链接变量 A, B, C, D，将其分别与初始变量进行下模 2322^{32} 加法，转换为十六进制拼接起来，最后分别进行小端序反转即可获得最终 MD5 散列值。

@classmethod
def _step_5(cls):
    # Convert the buffers to little-endian.
    A = struct.unpack("<I", struct.pack(">I", cls._buffers[MD5Buffer.A]))[0]
    B = struct.unpack("<I", struct.pack(">I", cls._buffers[MD5Buffer.B]))[0]
    C = struct.unpack("<I", struct.pack(">I", cls._buffers[MD5Buffer.C]))[0]
    D = struct.unpack("<I", struct.pack(">I", cls._buffers[MD5Buffer.D]))[0]
    # Output the buffers in lower-case hexadecimal format.
    return f"{format(A, '08x')}{format(B, '08x')}{format(C, '08x')}{format(D, '08x')}"

一些问题

大端序与小端序

字节存储顺序主要分为大端序（Big-endian）和小端序（Little-endian），区别如下：

  • Big-endian：高位字节存入低地址，低位字节存入高地址；

  • Little-endian：低位字节存入低地址，高位字节存入高地址。

例：将 12345678h 写入 1000h 开始的内存中，以大端序和小端序模式存放结果如下：

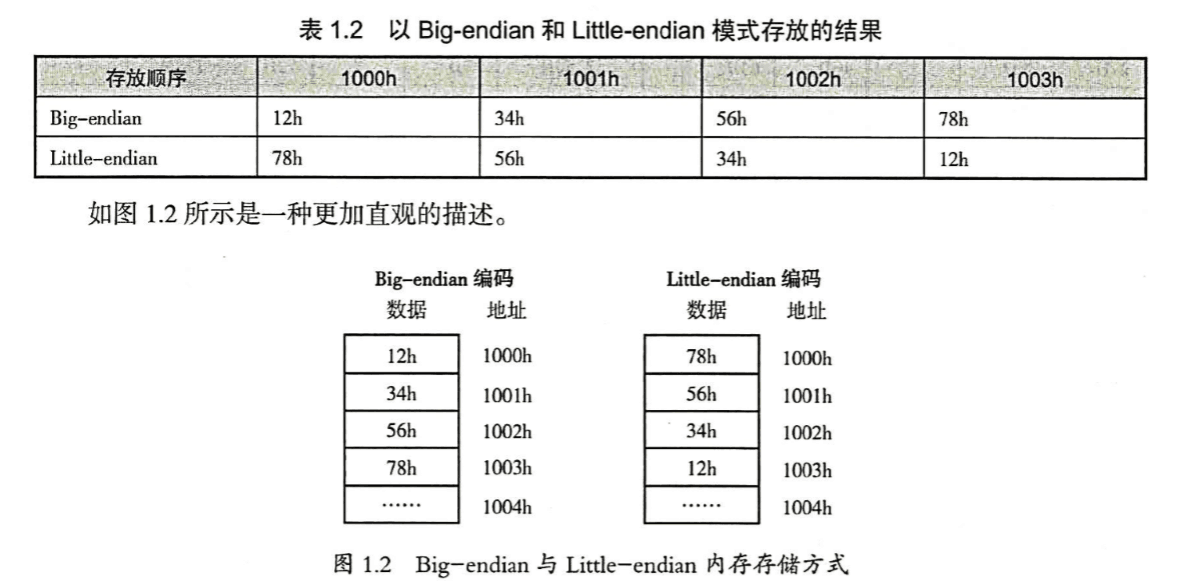
一般来说，x86 系列 CPU 都是 Little-endian 字节序，PowerPC 通常是 Big-endian 字节序，因为网络协议也都是采用 Big-endian 方式传输数据的，所以有时也把Big-endian 方式称为 网络字节序。

-*- 完整 Python 代码：

# -*- coding: utf-8 -*- 

import struct
from enum import Enum
from bitarray import bitarray
from math import (
    floor,
    sin,
)

class MD5Buffer(Enum):
    A = 0x67452301
    B = 0xEFCDAB89
    C = 0x98BADCFE
    D = 0x10325476

class MD5(object):
    _string = None
    _buffers = {
        MD5Buffer.A: None,
        MD5Buffer.B: None,
        MD5Buffer.C: None,
        MD5Buffer.D: None,
    }

    @classmethod
    def hash(cls, string):
        cls._string = string

        preprocessed_bit_array = cls._step_2(cls._step_1())
        cls._step_3()
        cls._step_4(preprocessed_bit_array)
        return cls._step_5()

    @classmethod
    def _step_1(cls):
        # Convert the string to a bit array.
        # 将字符串转化为二进制数组(Big-endian)
        bit_array = bitarray(endian="big")
        bit_array.frombytes(cls._string.encode("utf-8"))
        # Pad the string with a 1 bit and as many 0 bits required such that
        # the length of the bit array becomes congruent to 448 modulo 512.
        # Note that padding is always performed, even if the string's bit
        # length is already conguent to 448 modulo 512, which leads to a
        # new 512-bit message block.
        bit_array.append(1)
        while bit_array.length() % 512 != 448:
            bit_array.append(0)
        # For the remainder of the MD5 algorithm, all values are in
        # little endian, so transform the bit array to little endian.
        return bitarray(bit_array, endian="little")

    @classmethod
    def _step_2(cls, step_1_result):
        # Extend the result from step 1 with a 64-bit little endian
        # representation of the original message length (modulo 2^64).
        length = (len(cls._string) * 8) % pow(2, 64)
        length_bit_array = bitarray(endian="little")
        length_bit_array.frombytes(struct.pack("<Q", length))

        result = step_1_result.copy()
        result.extend(length_bit_array)
        return result

    @classmethod
    def _step_3(cls):
        # Initialize the buffers to their default values.
        for buffer_type in cls._buffers.keys():
            cls._buffers[buffer_type] = buffer_type.value

    @classmethod
    def _step_4(cls, step_2_result):
        # Define the four auxiliary functions that produce one 32-bit word.
        F = lambda x, y, z: (x & y) | (~x & z)
        G = lambda x, y, z: (x & z) | (y & ~z)
        H = lambda x, y, z: x ^ y ^ z
        I = lambda x, y, z: y ^ (x | ~z)

        # Define the left rotation function, which rotates `x` left `n` bits.
        rotate_left = lambda x, n: (x << n) | (x >> (32 - n))

        # Define a function for modular addition.
        modular_add = lambda a, b: (a + b) % pow(2, 32)

        # Compute the T table from the sine function. Note that the
        # RFC starts at index 1, but we start at index 0.
        T = [floor(pow(2, 32) * abs(sin(i + 1))) for i in range(64)]

        # The total number of 32-bit words to process, N, is always a
        # multiple of 16.
        N = len(step_2_result) // 32

        # Process chunks of 512 bits.
        for chunk_index in range(N // 16):
            # Break the chunk into 16 words of 32 bits in list X.
            start = chunk_index * 512
            X = [step_2_result[start + (x * 32) : start + (x * 32) + 32] for x in range(16)]

            # Convert the `bitarray` objects to integers.
            X = [int.from_bytes(word.tobytes(), byteorder="little") for word in X]

            # Make shorthands for the buffers A, B, C and D.
            A = cls._buffers[MD5Buffer.A]
            B = cls._buffers[MD5Buffer.B]
            C = cls._buffers[MD5Buffer.C]
            D = cls._buffers[MD5Buffer.D]

            # Execute the four rounds with 16 operations each.
            for i in range(4 * 16):
                if 0 <= i <= 15:
                    k = i
                    s = [7, 12, 17, 22]
                    temp = F(B, C, D)
                elif 16 <= i <= 31:
                    k = ((5 * i) + 1) % 16
                    s = [5, 9, 14, 20]
                    temp = G(B, C, D)
                elif 32 <= i <= 47:
                    k = ((3 * i) + 5) % 16
                    s = [4, 11, 16, 23]
                    temp = H(B, C, D)
                elif 48 <= i <= 63:
                    k = (7 * i) % 16
                    s = [6, 10, 15, 21]
                    temp = I(B, C, D)

                # The MD5 algorithm uses modular addition. Note that we need a
                # temporary variable here. If we would put the result in `A`, then
                # the expression `A = D` below would overwrite it. We also cannot
                # move `A = D` lower because the original `D` would already have
                # been overwritten by the `D = C` expression.
                temp = modular_add(temp, X[k])
                temp = modular_add(temp, T[i])
                temp = modular_add(temp, A)
                temp = rotate_left(temp, s[i % 4])
                temp = modular_add(temp, B)

                # Swap the registers for the next operation.
                A = D
                D = C
                C = B
                B = temp

            # Update the buffers with the results from this chunk.
            cls._buffers[MD5Buffer.A] = modular_add(cls._buffers[MD5Buffer.A], A)
            cls._buffers[MD5Buffer.B] = modular_add(cls._buffers[MD5Buffer.B], B)
            cls._buffers[MD5Buffer.C] = modular_add(cls._buffers[MD5Buffer.C], C)
            cls._buffers[MD5Buffer.D] = modular_add(cls._buffers[MD5Buffer.D], D)

    @classmethod
    def _step_5(cls):
        # Convert the buffers to little-endian.
        A = struct.unpack("<I", struct.pack(">I", cls._buffers[MD5Buffer.A]))[0]
        B = struct.unpack("<I", struct.pack(">I", cls._buffers[MD5Buffer.B]))[0]
        C = struct.unpack("<I", struct.pack(">I", cls._buffers[MD5Buffer.C]))[0]
        D = struct.unpack("<I", struct.pack(">I", cls._buffers[MD5Buffer.D]))[0]

        # Output the buffers in lower-case hexadecimal format.
        return f"{format(A, '08x')}{format(B, '08x')}{format(C, '08x')}{format(D, '08x')}"

if __name__ == "__main__":
    while True:
        msg = input("Please Input Your Message >> ")
        cipher = MD5.hash(msg)
        print(f"> MD5(\"{format(msg)}\") = {format(cipher)}")
RSS