3ND

Hill Cipher

希尔密码是运用基本矩阵论原理的替换密码，由 Lester S. Hill 在 1929 年发明。

每个字母当作 26 进制数字：$A=0, B=1, C=2...$ 一串字母当成 $n$ 维向量，跟一个 $n×n$ 的矩阵相乘，再将得出的结果模 26。

注意用作加密的矩阵（即密匙）在 {\mathbb {Z\}\}_{26}^{n} 必须是可逆的，否则就不可能解码。只有矩阵的行列式和 26 互质，才是可逆的。

* 编码:

* 解码:

Python 实现

• 字母表、字符串与矩阵的转化

alpha26 = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"

def stringToMatrix(string, alpha, size):
    rows = [[] for _ in range(size)]
    for i in range(len(string)-1): # -1 Remove /r
        rows[i % size].append(alpha.index(string[i]))
    return sp.Matrix(rows)

def matrixToString(matrix, alpha, size):
    string = ""
    for i in range(matrix.cols):
        for j in matrix.col(i):
            string += alpha[j % len(alpha)]
    return string

• 加密函数

矩阵模逆运算采用 Sympy 库进行，SymPy 是一个符号计算的 Python 库。它的目标是成为一个全功能的计算机代数系统，同时保持代码简洁、易于理解和扩展。它完全由Python 写成，不依赖于外部库。 SymPy 支持符号计算、高精度计算、模式匹配、绘图、解方程、微积分、组合数学、离散数学、几何学、概率与统计、物理学等方面的功能。

将明文字符串转化为矩阵后与 $n*n$ 密钥矩阵进行码表内的模乘，得到的加密矩阵转化为密文字符串即可。

import sympy as sp

def encrypt(plain, key_enc, alpha):
    key_enc = sp.Matrix(key_enc)
    # Calculate the Determinant and Check if there is a solution
    D = key_enc.det()
    if sp.gcd(D, 26) != 1:
        print "Not relatively prime. No solution!"
        exit()
    # Convert plain text to Matrix to Encrypt
    mat_plain = stringToMatrix(plain, alpha, key_enc.shape[0])
    # Calculate the Cipher Matrix
    mat_cipher = key_enc * mat_plain
    # Calculate the Cipher
    cipher = matrixToString(mat_cipher, alpha, key_enc.shape[0])
    return cipher

• 解密函数

根据密钥求解密钥矩阵的模逆作为解密矩阵与密文矩阵相乘即可获取明文矩阵。

def crack(cipher, key_enc, alpha):
    # Konw Cipher and Key_Enc to Crack Plain
    key_enc = sp.Matrix(key_enc)
    # Calculate the Key_Dec 
    key_dec = key_enc.inv_mod(len(alpha))
    key_dec = key_dec.applyfunc(lambda x: x % len(alpha))
    return encrypt(cipher, key_dec, alpha)

• 完整代码

#-*- coding: utf-8 -*-
# Hill Cipher By 3ND
import sympy as sp

alpha26 = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"

def stringToMatrix(string, alpha, size):
    rows = [[] for _ in range(size)]
    for i in range(len(string)-1): # -1 Remove /r
        rows[i % size].append(alpha.index(string[i]))
    return sp.Matrix(rows)

def matrixToString(matrix, alpha, size):
    string = ""
    for i in range(matrix.cols):
        for j in matrix.col(i):
            string += alpha[j % len(alpha)]
    return string

def encrypt(plain, key_enc, alpha):
    key_enc = sp.Matrix(key_enc)
    # Calculate the Determinant and Check if there is a solution
    D = key_enc.det()
    if sp.gcd(D, 26) != 1:
        print "Not relatively prime. No solution!"
        exit()
    # Convert plain text to Matrix to Encrypt
    mat_plain = stringToMatrix(plain, alpha, key_enc.shape[0])
    # Calculate the Cipher Matrix
    mat_cipher = key_enc * mat_plain
    # Calculate the Cipher
    cipher = matrixToString(mat_cipher, alpha, key_enc.shape[0])
    return cipher

def decrypt(cipher, key_dec, alpha):
    key_dec = sp.Matrix(key_dec)
    mat_cipher = stringToMatrix(cipher, alpha, key_dec.shape[0])
    mat_plain = key_dec * mat_cipher
    plain = matrixToString(mat_plain, alpha, key_dec.shape[0])
    return plain

def crack(cipher, key_enc, alpha):
    # Konw Cipher and Key_Enc to Crack Plain
    key_enc = sp.Matrix(key_enc)
    # Calculate the Key_Dec 
    key_dec = key_enc.inv_mod(len(alpha))
    key_dec = key_dec.applyfunc(lambda x: x % len(alpha))
    return encrypt(cipher, key_dec, alpha)

if __name__=="__main__":
    # Input Plain Text
    plain = raw_input("Input Plain Text >> ")
    # plian = 'ACT'
    # Input Key to Encrypt
    key_enc = input("Input Your Key Matrix >> ")
    key_enc = [[6, 24, 1], [13, 16, 10], [20, 17, 15]]
    # Encrypt
    print encrypt(plain, key_enc, alpha26)
    # POH
    # Input Cipher Text
    cipher = raw_input("Input Cipher Text >> ")
    # cipher = POH
    key_dec = input("Input Your Key Matrix >> ")
    key_dec = [[8, 5, 10], [21, 8, 21], [21, 12, 8]]
    print decrypt(cipher, key_dec, alpha26)
    # ACT
    # Input Cipher to Crack
    cipher = raw_input("Input Cipher Text (Crack)>> ")
    # Input the Key_Enc Matrix
    key_enc = input("Input Your Key_Enc Matrix >> ")
    key_enc = [[6, 24, 1], [13, 16, 10], [20, 17, 15]]
    print crack(cipher, key_enc, alpha26)

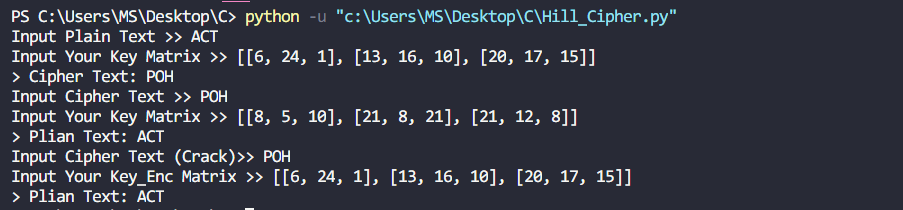
运行测试：